Oil & Gas Pipeline Survey
Wechselwirkungen zwischen Seeböden und Pipeline
Auf dem See- oder Meeresboden verlegte Offshore-Pipelines sind hydrodynamischen und zyklischen Betriebsbelastungen ausgesetzt. Infolgedessen können sie Instabilitäten am Boden, Wanderungen und seitliches Ausbeulen erfahren. Finite-Elemente-Simulationen sind in verschiedenen Phasen des Pipeline-Designs erforderlich, um die verschiedenen Belastungsfälle zu überprüfen.
Der Rohrleitungsentwurf hängt von der genauen Modellierung der axialen und lateralen Bodenwiderstände ab.
Konventionelle Pipeline-Konstruktionspraxis ist es, die Wechselwirkung zwischen Rohr und Meeresboden mit einfachen "Feder-Schieber"-Elementen in Abständen entlang des Rohres zu modellieren, da Finite-Elemente-Methoden mit ausgearbeiteten Kontakt- und Schnittstellenelementen zwischen der Pipeline und dem Fundament eine umfassende Modellierung langer Pipelinesysteme mit der derzeitigen Rechenleistung nicht zulassen (Tian et al., 2008).
Diese "Feder-Gleiter"-Elemente bieten eine bi-lineare, linear-elastische, perfekt plastische Reaktion in axialer und lateraler Richtung. Die begrenzenden axialen und lateralen Kräfte basieren auf empirischen Reibungsmodellen, die den axialen und lateralen Widerstand mit der vertikalen Bodenreaktion in Beziehung setzen, indem sie einen "Reibungsfaktor" verwenden.
In vertikaler Richtung wird üblicherweise eine aus der Tragfähigkeitstheorie abgeleitete nichtlineare elastische Lastverlagerungsreaktion angenommen, wobei die Rohrleitung als Flächenstreifenfundament behandelt wird, dessen Breite gleich der Querschnittslänge des Rohr-Boden-Kontakts an der angenommenen Verlagerung ist.
Diese einfachen Modelle können für Sand angemessen sein, sind aber für Ton, insbesondere weichen Ton, zu einfach. Wegen der langsamen Verfestigungsrate von Ton sollte ein Totalspannungsansatz mit einer undrainierten Scherfestigkeit su verwendet werden. In diesem Fall hängen die axialen und lateralen Widerstände nicht direkt von der vertikalen Bodenreaktion ab, sondern von der Kontaktfläche zwischen dem Rohr und dem Meeresboden. Folglich wird eine genaue Vorhersage der Rohrleitungseinbettung, die bei sehr weichem Untergrund groß sein kann, von vorrangiger Bedeutung.
Diese einfachen Modelle wurden verbessert, um die Einbettung der Pipeline sowie die axialen und lateralen Widerstände besser vorhersagen zu können, und wurden in ein Finite-Elemente-Softwareprogramm für die Pipeline-Analyse implementiert, um die Rohr-Boden-Interaktion von oberirdisch verlegten Pipelines in weichem Ton besser zu simulieren und die vollständigen Routen genauer zu simulieren.
Die neuen Funktionen werden in diesem Papier kurz erläutert. Ein neueres vertikales Rohr-Boden-Reaktionsgesetz, das die Entladung von Kunststoffen modelliert, ist in das Programm integriert. Es berücksichtigt Verlege- und dynamische Installationseffekte, um eine repräsentativere Rohrleitungseinbettung zu berechnen. Der axiale und laterale Widerstand ist jetzt mit der Rohrleitungseinbettung verknüpft. Schließlich werden die Gesetze der axialen und lateralen Spitzenrestwiderstände implementiert.
Vertikales Reaktionsgesetz
Lösungen zur Schätzung des Resistenzprofils wurden von Murff et al. (1989), Aubeny et al. (2005) und Randolph & White (2008) bereitgestellt. Die Rohrleitungsdurchdringung z kann aus der konventionellen Tragfähigkeitsgleichung, modifiziert für die gekrümmte Form einer Rohrleitung, geschätzt werden:
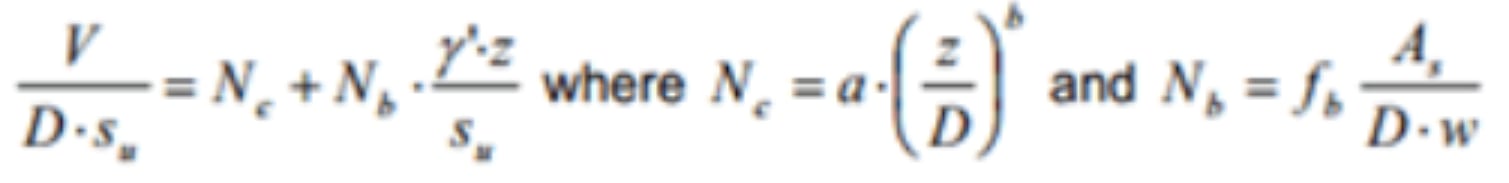
wobei V die vertikale Belastung pro Längeneinheit, D der Rohrleitungsdurchmesser, su die undrainierte Scherfestigkeit an der Rohrleitungsumkehrung und As die nominale untergetauchte Fläche des Rohrleitungsquerschnitts ist.
Für den Entwurf kann der Tragfähigkeitsfaktor Nc unter Verwendung gerundeter Werte der Potenzgesetz-Koeffizienten a und b geschätzt werden, zum Beispiel a = 6 und b = 0,25 (Randolph & White, 2008).
Bei extrem weichen Bodenverhältnissen hat der Auftrieb einen Einfluss. Dies wird durch den Auftriebsfaktor Nb erfasst. Der Faktor fb sollte wegen des Auftriebs gleich 1,5 genommen werden (Randolph & White, 2008).
Die Genauigkeit dieses Berechnungsansatzes, in der Größenordnung von +/- 10%, ist angesichts der anderen Unsicherheiten, wie z.B. der Installationseffekte, die die vertikale Last V (siehe unten) beeinflussen, ausreichend (White & Randolph, 2007).
Auswirkungen der Installation
Während der Installation einer Pipeline führen die vertikale und horizontale Bewegung des Verlegeschiffes und die Lastkonzentration beim Aufsetzen des Rohres zu einer größeren Eindringtiefe, als auf der Grundlage des eingetauchten Einheitsgewichts des Rohres berechnet wurde. Die Lastkonzentration kann durch Multiplikation des Rohrgewichts mit einem Verstärkungsfaktor flay, wie von Bruton (2006) vorgeschlagen, berücksichtigt werden.
Um den Effekt der Rohrbewegung während der Installation zu berücksichtigen, kann statt der intakten Festigkeit eine teilweise umgeformte Scherfestigkeit zur Berechnung der Rohreinbettung verwendet werden, wie von Dendani & Jaeck (2007) vorgeschlagen. Diese Merkmale in Kombination mit dem oben beschriebenen vertikalen Reaktionsgesetz ermöglichen die Vorhersage einer realistischeren Rohrleitungseinbettung, was für die Berechnung einer realistischen axialen und lateralen Festigkeit von größter Bedeutung ist.
Entladung von Kunststoff
Für die vertikale Erdfreiheit wird konventionell ein nichtlineares elastisches Lastverlagerungsverhalten angenommen. Es ist jedoch wichtig, eine Feder als sich plastisch verhaltend zu modellieren, um zu vermeiden, dass ein unrealistischer Rückprall vorhergesagt wird, wenn das Rohr unbelastet ist. In der Praxis wird ein Rohr oft überpenetriert, was bedeutet, dass sein Betriebsgewicht geringer ist als die maximale vertikale Kraft, die auf das Rohr ausgeübt wurde.
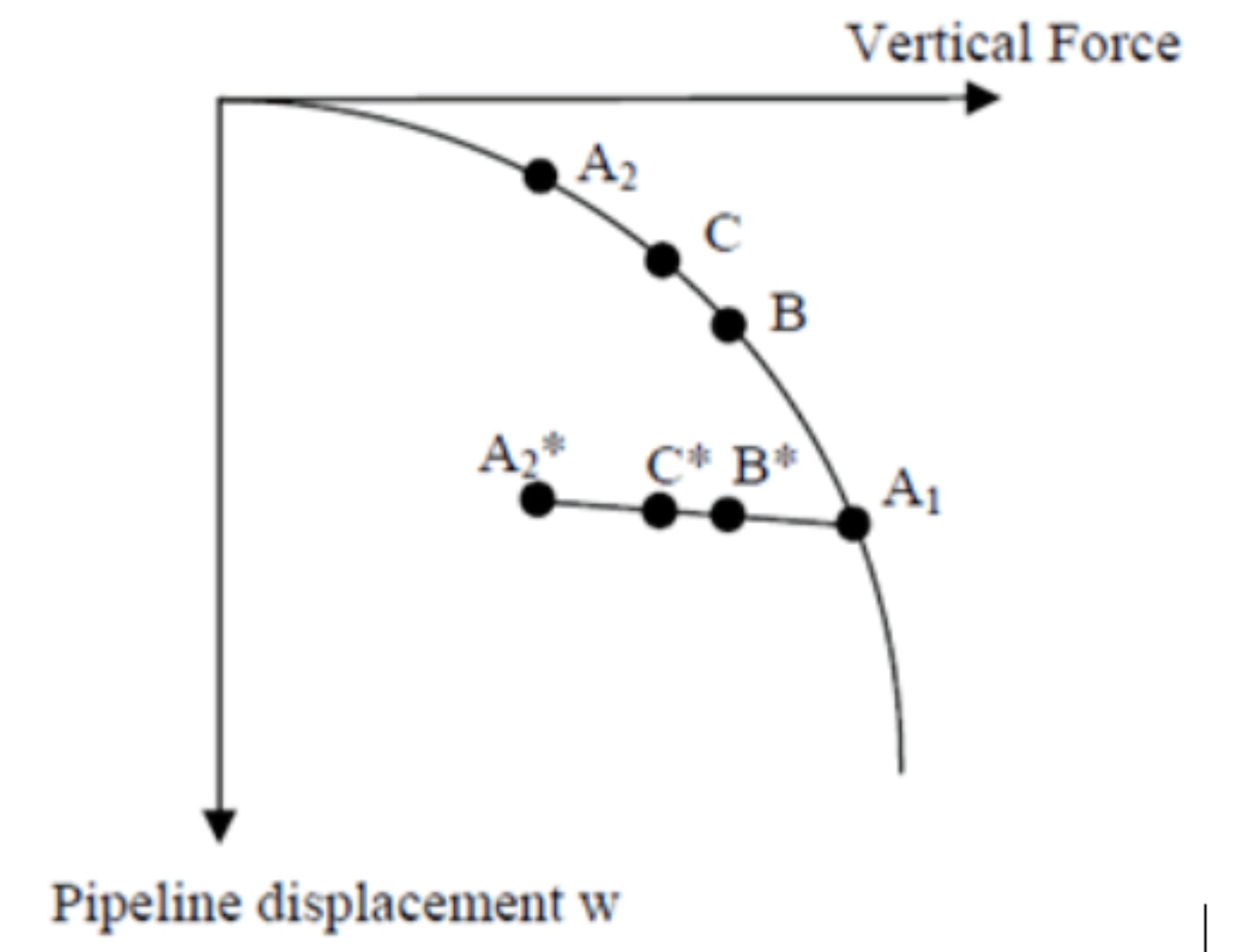
Tatsächlich wurde es entlastet. Es ist wichtig, eine Feder mit plastischem Verhalten und "Gedächtnis" zu modellieren, um die entsprechende vertikale Bodensteifigkeit zu berechnen. Das Verhalten eines übermäßig durchdrungenen Rohres kann durch die steife Entlastungs-/Entlastungslinie beschrieben werden. Wenn das Rohr bis zu seinem normal durchdrungenen Bereich nachbelastet wird, kann das Verhalten des Rohres so beschrieben werden, dass es der Einbettungskurve der unbelasteten Last folgt. Dies wird im folgenden Beispiel und in Abbildung 1 veranschaulicht.
Betrachten wir zunächst eine elastische Feder. Während der Installation bewegt sich das Rohr aufgrund der Lastkonzentration nach A1 und prallt dann nach A2 zurück, und zwar mit einer vertikalen Verschiebung, die seinem eingetauchten Leergewicht entspricht. Während des Hydrotests nimmt die vertikale Kraft zu und das Rohr bewegt sich nach B. Unter Betriebsbedingungen, wenn der Inhalt leichter als Wasser ist, wird das Rohr bis zu Punkt C entlastet.
Die Einbettung des Rohrs und die Tangentialsteifigkeit an diesem Punkt sind nicht realistisch. Im Falle einer elasto-plastischen Feder geht das Rohr während der Installation nach A1 und dann nach A2*, einer Entlastungs-Entlastungs-Linie folgend. Während des Hydrotests steigt die vertikale Kraft entlang der Entlastungs-Lastungs-Linie auf B* an.
Schließlich wird das Rohr nach C* entlastet. Zu diesem Zeitpunkt sind die Rohrleitungseinbettung und die Tangentialsteifigkeit realistischer. Eine genaue Rohrleitungseinbettung ist besonders wichtig, wenn sie an den axialen und lateralen Widerstand gekoppelt ist.
Kopplung von axialem und lateralem Widerstand mit Rohrleitungseinbettung
Kopplung von axialem und lateralem Widerstand mit Rohrleitungseinbettung
Die axialen und lateralen Widerstände hängen von der Kontaktfläche zwischen dem Rohr und dem Meeresboden und damit von der Rohrverankerung ab, wenn ein Totalspannungsansatz verfolgt wird. Die Formel, die zur Berechnung der Spitzenwerte der axialen und lateralen Widerstände Fpa und Fpl verwendet wird, liegt in der Form vor:
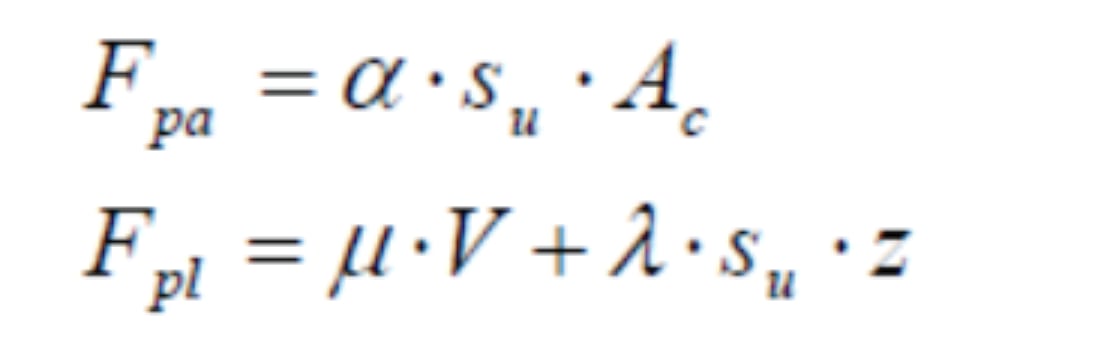
wobei αsu die Einheit der Grenzflächenschubfestigkeit ist, Ac ist die Kontaktfläche zwischen dem Rohr und dem Meeresboden, die eine Funktion der Rohrverankerung z ist, μ ist ein "Reibungsfaktor" im Bereich von 0,2-0,8 (Randolph & White, 2007) und
λ einen Koeffizienten, der typischerweise im Bereich von 0,5-2 liegt.
Die axialen und lateralen Widerstände wurden mit der Rohrleitungseinbettung verknüpft, so dass sie automatisch berechnet werden und sich während der Analyse ändern können.
Dreilineares axiales und laterales Modell
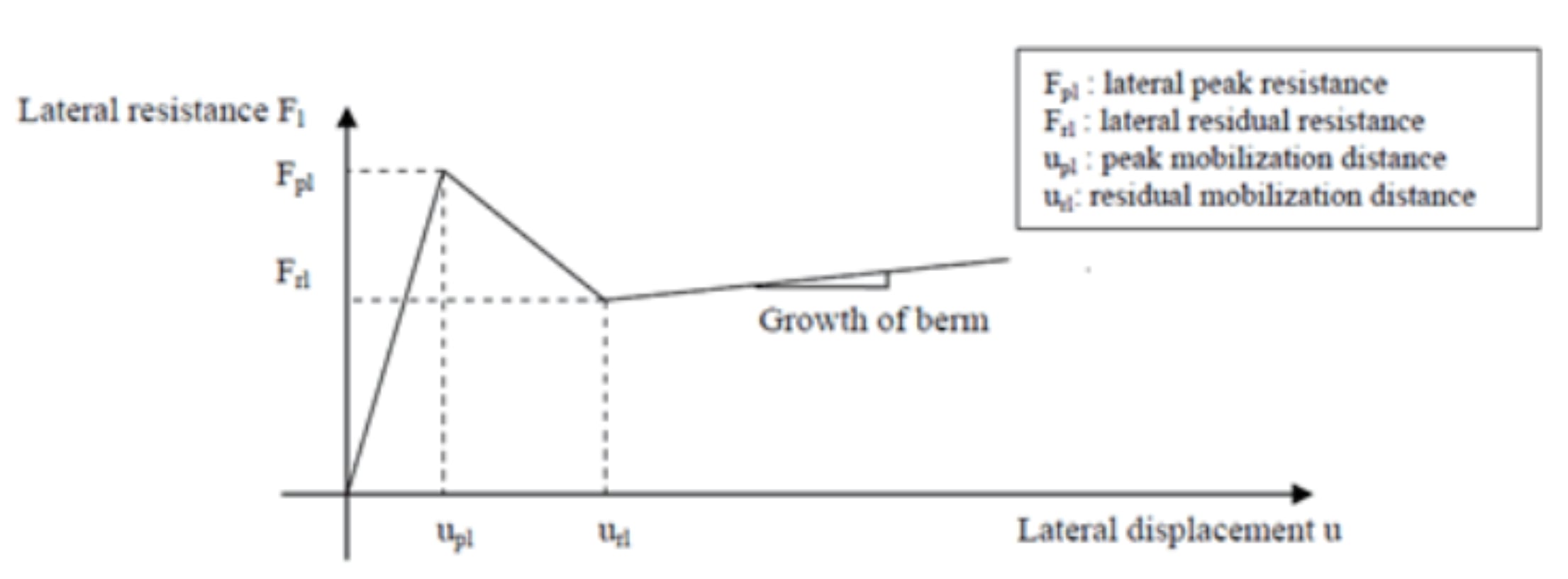
Die Modelle der einfachen bi-linearen axialen und lateralen Reibungswiderstände wurden verbessert, so dass sie Spitzen- und Restwiderstände verwenden können, um die Erweichung der axialen und lateralen Reaktion zu modellieren, die bei Ton häufig beobachtet wird. Wie bereits erläutert, werden Rohrleitungen in der Praxis oft zu stark penetriert.
Wenn dies bei weichem Ton auftritt, ist der seitliche Ausbruchswiderstand Fpl hoch und fällt stark ab, wenn der Sog an der Rückseite des Rohrs verloren geht, und nimmt dann weiter ab bis zu einem Restwert Frl, wenn das Rohr zu einer flacheren Einbettung ansteigt. Wenn der Restwiderstand erreicht ist, kann der seitliche Widerstand wieder ansteigen, weil sich vor dem Rohr eine Bodenberme bildet (siehe Abbildung 2). Auch der axiale Widerstand kann durch Sogfreisetzung und Tonumformung eine Dehnungserweichung erfahren.
Scan4Pipes Europe GmbH
Umgehungsstraße 78b - Hauptgebäude
D-99441 Mellingen
Germany
E-Mail: office@scan4pipes.com
Phone: +49 176 346 928 81
Website: scan4pipes.com
© Scan4Pipes Europe GmbH 2019 - 2023
Steuernummer: 162/118/05297
USt.-IdNr.: DE328138499
Registergericht: Jena
Handelsregister: HRB 516297